Minecraft Redstone Decimal Carry Cancel Adder(part1)

こんにちはー(･ω･*)ﾉﾉ

計算機を制作していたのですが、cloneミスで計算機が吹っ飛んだり度重なるクラッシュで戦意喪失したので解説を投げて私の受験が終わるまで制作を中断しようと思います(;´д｀)

基礎的な論理回路と2進数の加算器は既知として説明しますが、他何か不詳な点あれば説明を足すので指摘ください!

作り方は最後の方にあります。

タイトルのCarry Cancel Adder(CCA)とは外国人のMajic氏が開発した2進数加算器(binary adder)であり、2進数14bitの加算が繰り上がり(carry)の遅延が無いという凄すぎる技術を天才すぎるアイデアで実現したものである。元動画リンク:

youtu.be

しかし、5年経った今でも知名度が低いのが現状である。私は丁度3年前にこの2進数の加算器を10進数の連続加算器(decimal loop adder)にかなり時間をかけて改良し、加算を何回も出来るようにした。CCA(Carry Cancel Adder)の説明をした後、連続加算器があれば乗除算を高速かつ同じマシンで出来るようになる方法があるので紹介したい次第である。最終的には三角関数計算機の解説を目標とする。便宜上数式を使うが、実際の理解としては感覚に近いと思う。

信号強度半加算器

信号強度加算器では信号強度とデータの値を対応させて、コンパレータの減算モードを何個か用いて計算するもので、2進数と半加算器が2つ並んで全加算器を構成し、全加算器が加算器を構成していることと似ている。

コンパレータ減算モードの挙動は、背面,側面の入力,出力をそれぞれ $a,b,c$ として $c=R(a-b)$ と表される。

ここで $R$ はRamp関数であり $R(x)=x(x≧0),R(x)=0(\rm{それ以外のとき} )$

$0≦a,b≦9$ の整数の加算について見ていく。

$a+b≦9$ のとき $a+b=9-(9-b-a)$ となるが、値の範囲を確かめれば

$a+b=R(9-R(R(9-b)-a))$ となることが確認出来ると思う。

$a+b≧10$ のとき1の位の値は $a+b-10=a-(10-b)$ なので

$a+b-10=R(a-R(9-b))-1$ で表せる。2つの数式を見比べると、共通して $R(9-b)$ という部分が含まれているので、ここから回路を小型化できそうだと私は昔閃いた。 $R(x-y)$ の形をコンパレータ減算モードだと思えば、数式に従って次のように回路が実現できる。(-1は強度1減衰と考える)

[図2]

f:id:AkaGhef:20200608074744p:image

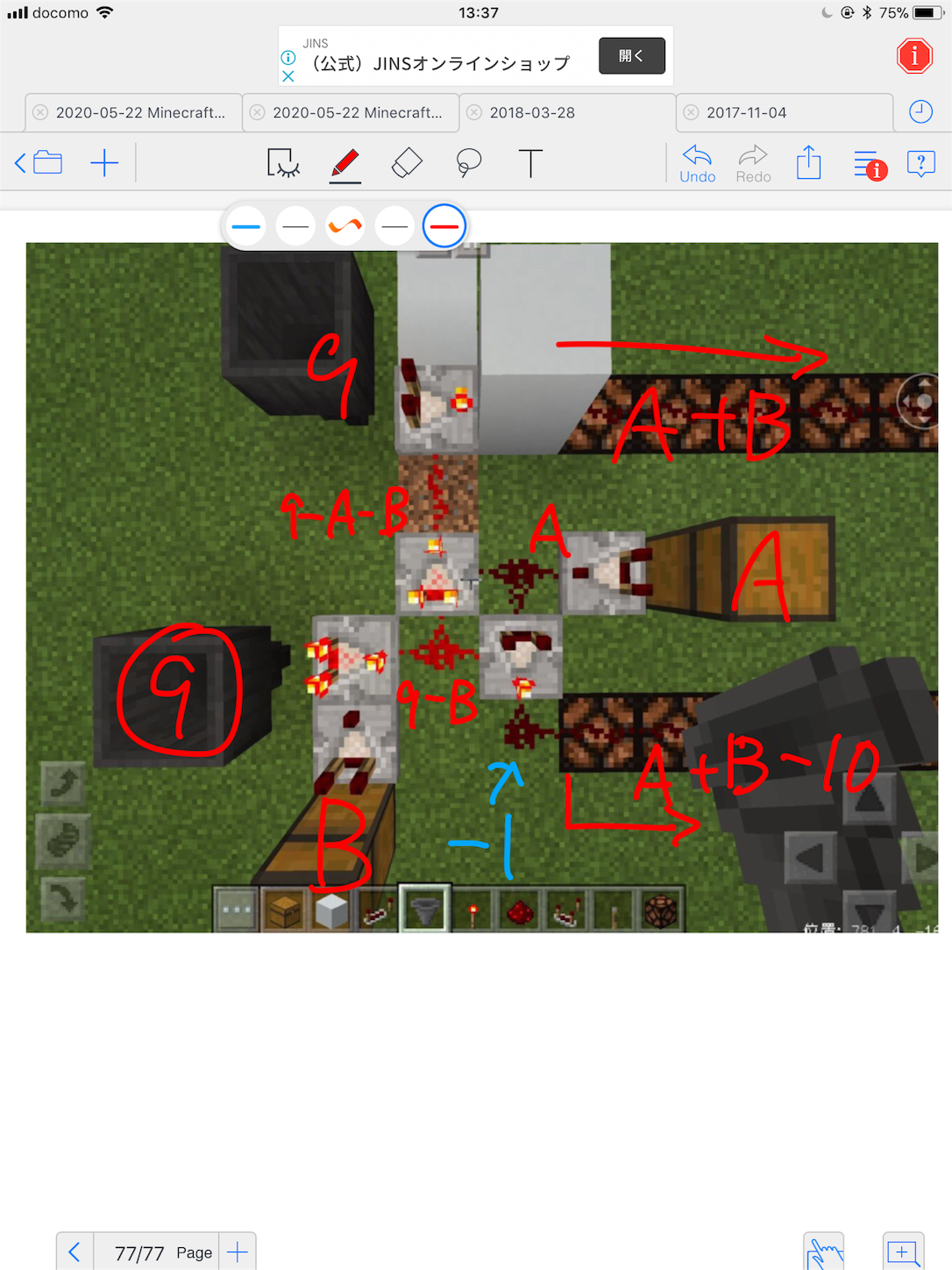
この回路は下位からの繰り上がりを考慮していないので半加算器と呼ぶ。2進数の場合は半加算器を2つ並べて、ある桁の入力 $a,b$ ,下位からの入力 $C^i$ からその桁の出力 $O$ ,上位桁への繰り上がり出力 $C^o$ を出力する全加算器を構成している。10進数の場合は全加算器は半加算器1つと、 $C^i$ を考えた $+1,+0$ の操作をする部分に分かれる。

CCA 繰り上がり計算機構

ここからがCCAの枢要たる部分だが、 $12$ 桁程度の加算では全ての $C^i$ を各桁の $a,b$ から瞬時に計算できるのである。加算の筆算では下位桁から順に計算するように、加算する桁数に比例して計算に時間がかかるので、全体の計算時間のネックとなるのでここを高速化する必要がある。アイデアは冒頭で挙げたリンク先から得たもので、加算器の理論を後から知ったのでそれを加えて解説していこうと思う。下位から第 $k$ 桁目の $a,b,C^i,C^o$ 値をそれぞれ $A_k,B_k,C_k^i,C_k^o$ と書く。

現実の々加算器には高速化の手段としてCarry Look Aheadがありその中にPG信号という理論がある。繰り上がりがどう上位の桁に影響を及ぼすかを見るために、各桁について"propagate"か"generate"という概念を定める。 $N$ 進法( $N=2,10$ で十分)の加算で、 $A_k+B_k=N-1$ であるとき、第 $k$ 桁はpropagate状態、(P)という。また、 $A_k+B_k≧N$ のとき、generate状態、(G)という。本解説では便宜をはかって、(P)でも(G)でもないとき、cancel状態、(Cc)と呼ぶことにする。(P)、(G)、(Cc)は排反(2つが同時に起こり得ることは無い)で、いずれかひとつの状態である。足し算の筆算を書きまくって確かめて欲しいが、具体例を1つ書いた。

[図4]

f:id:AkaGhef:20200606024845j:image

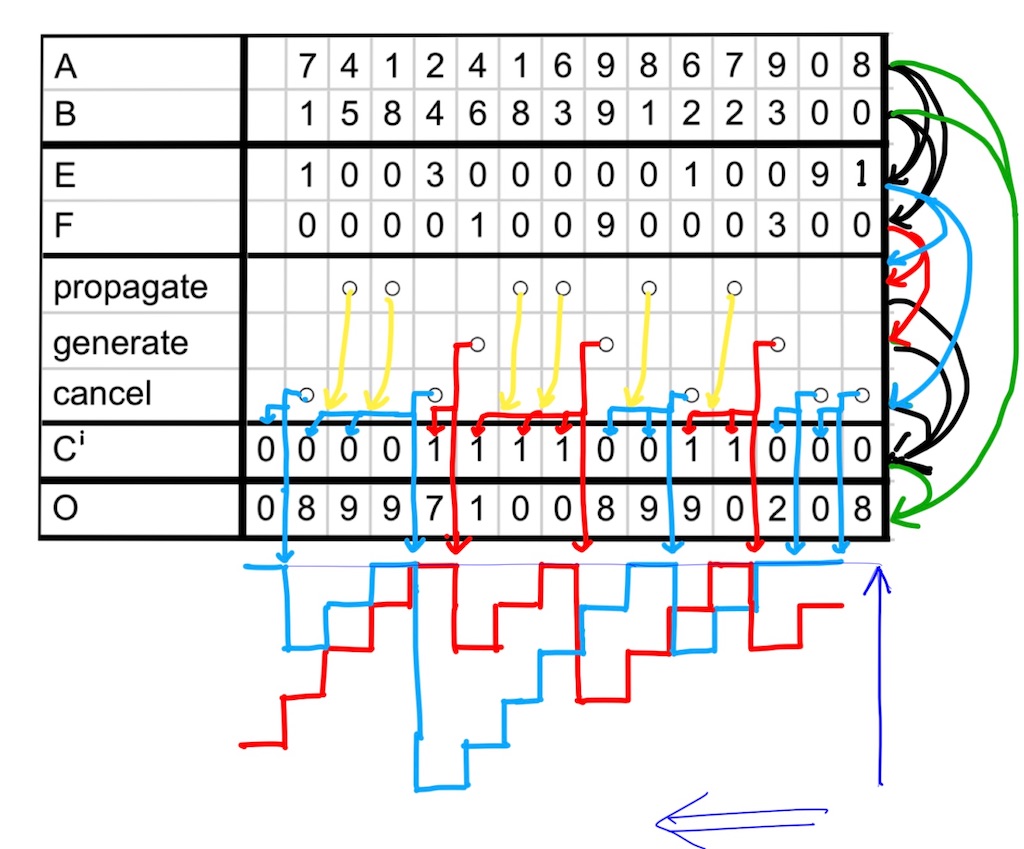
CCAでは2本の信号強度の配線の強度の大小関係で $C^i_k$ を決定しており、ワイヤーと大小関係を比較するコンパレータしかいらないので上位桁にもほぼ遅延無く情報が届き即座に $C^i$ の決定ができる。第 $k+1$ 桁が(P)であるとき $C^o_k=C^i_{k+2}$ が成り立つが、まさに第 $k$ 桁の繰り上がり出力が第 $k+1$ 桁をそのまま伝搬(propagate)し、第 $k+2$ 桁に入力されている。(G)は繰り上がりが発生(generate)すること意味し、(P)が続く限り伝搬し続ける。ここまでは現実の理論体型と同じだが、繰り上がりが発生しない(Cc)のときは「(P)が続く限り繰り上がりを阻止(cancel)する波が伝搬する」と捉えることで2本目の信号強度配線を導入したのである(私はそれまで1本だったので驚いた)。マイクラで回路を作成する際、(P)の伝搬は上位への一方通行であることに注意して、下の[図6]のように半blockを使って整流して下位に信号が流れないようにする(開発者の発想が天才すぎて泣く)

[図4]のように階段状の図を描き、(G)側の赤色のグラフと、(Cc)側の水色のグラフを規則に従って書いている。赤色のが水色より上側のとき $C^i=1$ で、逆ならば $C^i=0$ である。グラフの縦軸は信号強度を指し示しており、強度の大小関係をコンパレータで決定して $C^i$ を出力する。グラフの規則は、(G)があったときは赤色を上限値まで上げて、(Cc)があったときは水色を上限まで上げる。(P)であるとき(黄色矢印)は信号強度配線には何もせず、赤色と水色両方を1段階減衰させるが、大小関係は保存されている。

以上が $C^i$ 決定の流れである。半加算器をベースに、(P)、(G)、(Cc)のどれであるかを決定する回路を見ていく。 $E_k=R(R( (N-1) -B_k)-A_k)$ 、 $F_k=R(A_k-R ( (N-1) -B_k))$ としたときに、

$「k桁目が(P)」\Leftrightarrow E_k=F_k=0$

$「k桁目が(G)」\Leftrightarrow F_k≧1$

$「k桁目が(Cc) 」\Leftrightarrow E_k≧1$

となることを[図4]を見て確かめてみてほしい。

1以上か0であるかはリピーターやトーチで簡単に判定できるし、(P)はNOR回路である。CCAの機構を $E,F$ を用いて回路にするとこうなる。

[図6]

f:id:AkaGhef:20200607154501j:image

f:id:AkaGhef:20200607154506j:image

信号強度全加算器

最後のステップである加算結果を出力する回路について見てく。

$E$ は(Cc)のときの加算結果を計算する回路に使える、つまり繰り上がり入力を $C^i=0,1$ としたとき

$(Cc)\Rightarrow O=R(R(10-R(1-C^i))-E)$

である。 $F$ は(G)のときの加算結果を計算する回路に使える、つまり

$(G)\Rightarrow O=R(F-R(1-C^i))$

(P)のときはめんどくさいことが起きる。k桁目が(P)のとき半加算器の出力は $9$ で、 $C_k^i=0$ ならば $O_k=N-1$ だが $C_k^i=1$ ならば $O_k=0$ となるので、信号強度に $C^i$ を足し引きして $O$ を計算するわけには行かない。だから別途配線を用意する必要がある。

[図8]

f:id:AkaGhef:20200608083130j:image

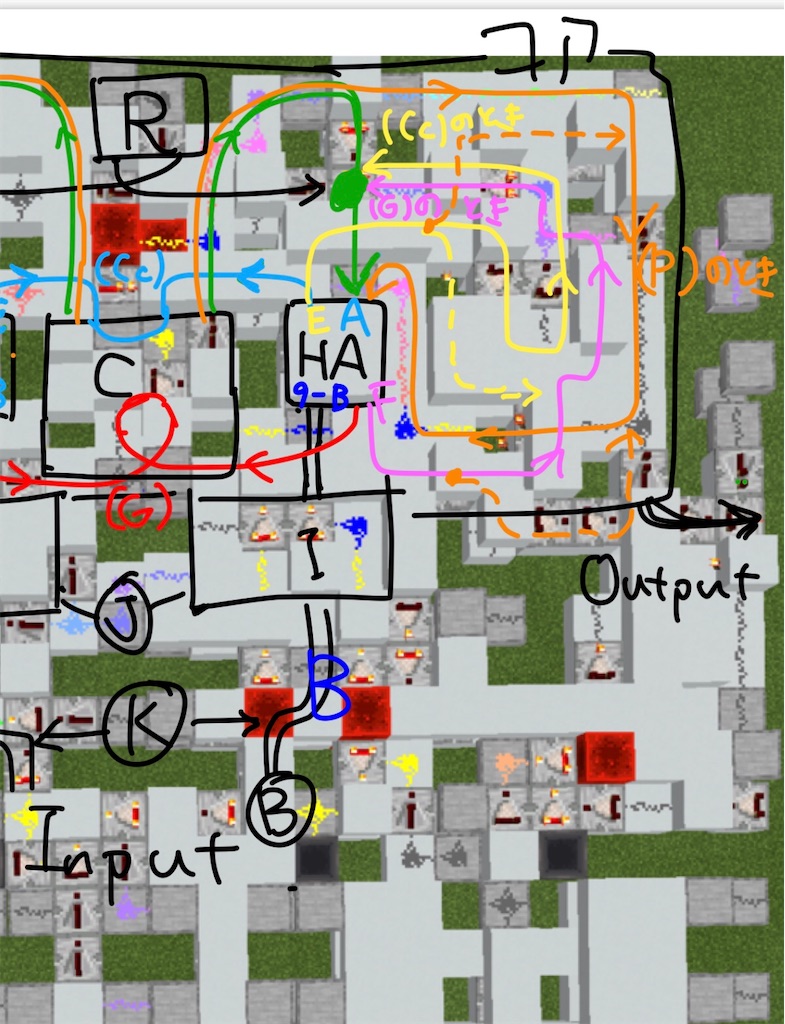
実際のマイクラの回路は上のようになる。(めんどくさいので)連続加算器の画像をそのまま使っているが、加算器も連続加算器も仕組みはほぼ同じで、加算結果 $O$ がそのまま $A$ に繋がれて代入されているという違いだけである。[HA]は半加算器、[C]はCCAの繰り上がりの計算機構、Bが入力、[R]はリセットの配線、[I]は $B$ を $9-B$ にする回路で、桁毎に何層も積み重なっている計算機の1桁分(2マス)だけ切り出してきた断面の画像である。さっきの[HA]でE,Fを計算し、(G)の繰り上がり計算部分は[図4]の階段のグラフの赤色と同じで、信号強度配線に繋がっている。(Cc)の繰り上がり計算のための信号強度配線は同じように水色である。(G)のときの加算結果はピンク色で、(Cc)のときは黄色、(P)のときは橙色の矢印で書いている。黄色破線は、 $E,F$ どちらの値を半加算器の出力として使うかを決定するものである。

[図8]の橙色破線は、(P)の時の $O$ を出力する部分の $E,F$ からの入力で、 $E=F=C^i=0$ のときは $O=9$ を出力するようになっている。[C]の部分から $C^i$ が出力され、(P)以外のときは水色の丸の部分で半加算器の値と $C^i$ から $O$ を計算している。[R]はリセットの配線で、Aの値を0にするが、ここの部分の回路だけ非同期なのでパイプライン処理出来ない。

パイプライン演算

パイプライン演算は計算機においてかなり重要な概念であるのでここで説明しておきたい。ループ式の計算回路で、信号を回路内で何周もさせて計算する際、信号の辿るルートによって遅延が異なる場合は周回する毎に遅延が拡大していき周回するうちに1周回遅れて前の信号と干渉してしまう。このためループ計算の回路において、「信号が回路を1周回して戻るときの遅延量は経路によらず等しい」という強い条件「同期」が必要となる。ここではループ計算において同期を定義したが、一般に信号の入力から出力までの遅延量が経路によらず等しければ同期式回路である。

同期式のループ回路において時刻毎に処理が独立していて、1rstick毎に違う信号を入力したとき何個もの計算をほぼ同時にやることが可能で、これをパイプライン処理と言う。信号が波形を崩さずに配線を伝搬していく様子が波に見えることから特にウェーブパイプラインと呼ばれる。マイクラの場合で注意すべきだが、遅延2のリピーターに1rstickパルスが入力された時に2rstickのパルスが出力されて前の時刻の信号と干渉してしまうため1tick毎に違う処理を行う際は2rstick遅延のリピーターは使用できないという制約が追加される。ウェーブ型以外もあって、遅延量が一定でない場合一旦バッファという領域に信号を保存し回路全体の時刻調整をする"クロック"の制御のもとで同時に情報を次の処理領域に渡したりする。

補数による減算

減算は補数の概念を使えば驚くほど楽に加算器上に実現できることが知られている。今回は信号強度加算器が主題なので、10進数N桁の整数 $x,y \lt 10^{N}$ の補数の計算から減算 $x-y$ を行う方法を考える。まず答えが正になる場合について見ることにし、 $yの10^n$ の位を $y_n$ と書くと $y=\displaystyle \sum_{n=0}^{N-1}10^{n}y_n$ と表せる。 $\overline{y}_k=9-y_k$ とし、さらに $\bar{y}=\displaystyle \sum_{n=0}^{N-1}10^n \overline{y}_n$ と定義する。 $y$ の補数とは $\overline{y}+1$ であり簡単な計算から

$\displaystyle \overline{y}=10^N-y-1=(\underbrace{99\cdots 9}_{9がN個}-y)$ と分かる。

$x-y=x+(\underbrace{99\cdots 9}_{9がN個}-y)+1-10^N$ となり、下位 $N$ 桁には影響が及ばないので $10^N$ を無視すると、 $x+\overline{y}+1$ という「足し算」を計算すればいいことになる。ここで $y$ から $\overline{y}$ を求めるには各桁で独立に $y_k$ から $\overline{y}_k$ を求めればいいので、すぐに求められる。

また、 $+1$ の部分は加算器の最下位桁の繰り上がり入力 $C_1^i$ が空いているので、ここから入力すれば良い(インクリメントをここで使うのか!と、最初知ったときは仰天した)

この加算を行うと、無視した $10^N$ の分があるので答えが正のとき必ず最上位桁の繰り上がりが起こる( $C_{N+1}^i=1$ )

e.g.) $512-128\rightarrow 512+871+1=1384\rightarrow 512-128=384$

逆に減算結果が負ならば最上位桁の繰り上がりが起こらず $C_{N+1}^i=0$ となるので、負になったかどうか判別できる。しかし減算結果の数字を出力するには絶対値を出力しなければならないので、加算結果の補数を見る必要がある(丁寧な説明が困難なので具体的な計算手順をみて掴んでください)

e.g.) $128-512→ 128+487+1=\underline{0}616\rightarrow \overline{616}+1=383+1=384$

$\rightarrow 128-512=-384$

一応数式を載せると、 $|x-y|=-(x-y)=10^N-(x+\overline{y}+1-10^N)-10^N=\overline{x+\overline{y}+1}+1$

しかし減算器単体として運用する場合は、加算結果の補数を求める際に+1(インクリメント)をしなければならず面倒なので連続加算器であることを利用した2つの解決方法を述べる。 $\overline{y}$ を $y$ の補数反転と呼ぶことにする(元々補数は2進数の概念で、補数を求める時は各桁でNOTゲートを通す、つまりbit反転すればよい)

ひとまず+1なしで加算を計算し $x+\overline{y}$ の加算で $C^i_{N+1}=1$ ならば+1をして出力、 $C^i_{N+1}=0$ ならば

補数反転を計算して出力する( $\overline{x+\overline{y}}$ )

$114-514\rightarrow 114+485=\underline{0}599→114-514=-\overline{599}=-400$

$514-114\rightarrow 514+885=\underline{1}399→514-114=399+1=400$

連続加算器なのでオーバーフローしなければ連続減算も可能で、引く時は減数の補数を加えると良いが、第2の方法としては総和結果が負になる場合、1を引く、すなわち補数である $\underbrace{99\cdots 9}_{9がN個}$ を加えてから、出力を補数反転させてやると絶対値が出る

e.g.) $137-343-729→(137+656+1)-729→0794+270+1=1065$

$065+999=1064→(\rm{answer})=-\overline{064}=-935$

私の計算機は当初から乗除算を前提として設計された為、加減算を同じマシンでできるようにしている。 $x+y$ と $x-y$ は補数にしてから足すかの違いなので、1つの入力で切り替えられるようにしている。それが[図8]における[I]の役割であり、(J)の部分で加算か減算かを制御している。(J)がonなら減算するモードになる。

最後に連続加算器全体の構造と作り方を見ていく。[図8]では少し説明を端折ったが[図12]のように加算器は下位桁から上位桁に向かって下側から左右交互ジグザグに桁が配置されていて(偶数桁目は右側という感じで)、CCAの機構を最大限活かして限界である10進数13桁(14もギリギリ)の構成になっている。ただこの加算器を2個上下に重ねて下側の加算器の最上位の繰り上がりのところを上側の加算器の最下位桁の繰り上がり入力に繋げれば2倍の桁数の加算器が作れる。また、交互に重ねずに2highずつ重ねていくと高さは半分で桁数が半分の7桁、横の長さが半分の連続加算器も作れる(ちと時間が無くて作れないので今は画像が無い )

[K]は入力Bをコア内に入力するかどうか決める配線で、[M]はシフトレジスタ(メモリ)、[S]はシフトする部分

出力する機構が少し面倒で、信号が内部を流れているのでF側の配線から信号取り出す必要がある。

$B$ に $99\cdots 9$ を代入する、または $B=0$ の状態で(J)をonにすると補数反転されて $99\cdots 9$ が代入される。そうすると[図8]のようにピンク色の配線に $A$ の強度の信号が流れるので、[output]と書いた部分から信号を取り出す。

[図10]

f:id:AkaGhef:20200608083140j:image

[図12]

f:id:AkaGhef:20200606222322j:image

各層は2highの厚さで、左右交互に桁が積み重なっているので、線対称な直線で切った[図14]を左右交互に積み重ねるようにして、cloneコマンドを実行すると13桁の計算機が出来上がる。1桁分に必要な回路の部分は[図8]の仕組みを理解していれば分かるだろう。

赤色の部分は乗除機を作る上で上から下に信号を送る必要があるのでそこの部分だけは螺旋状にワイヤーを設置する([図15]参照)

[図14]

f:id:AkaGhef:20200609233430j:image

[図15]

f:id:AkaGhef:20200609233444p:image

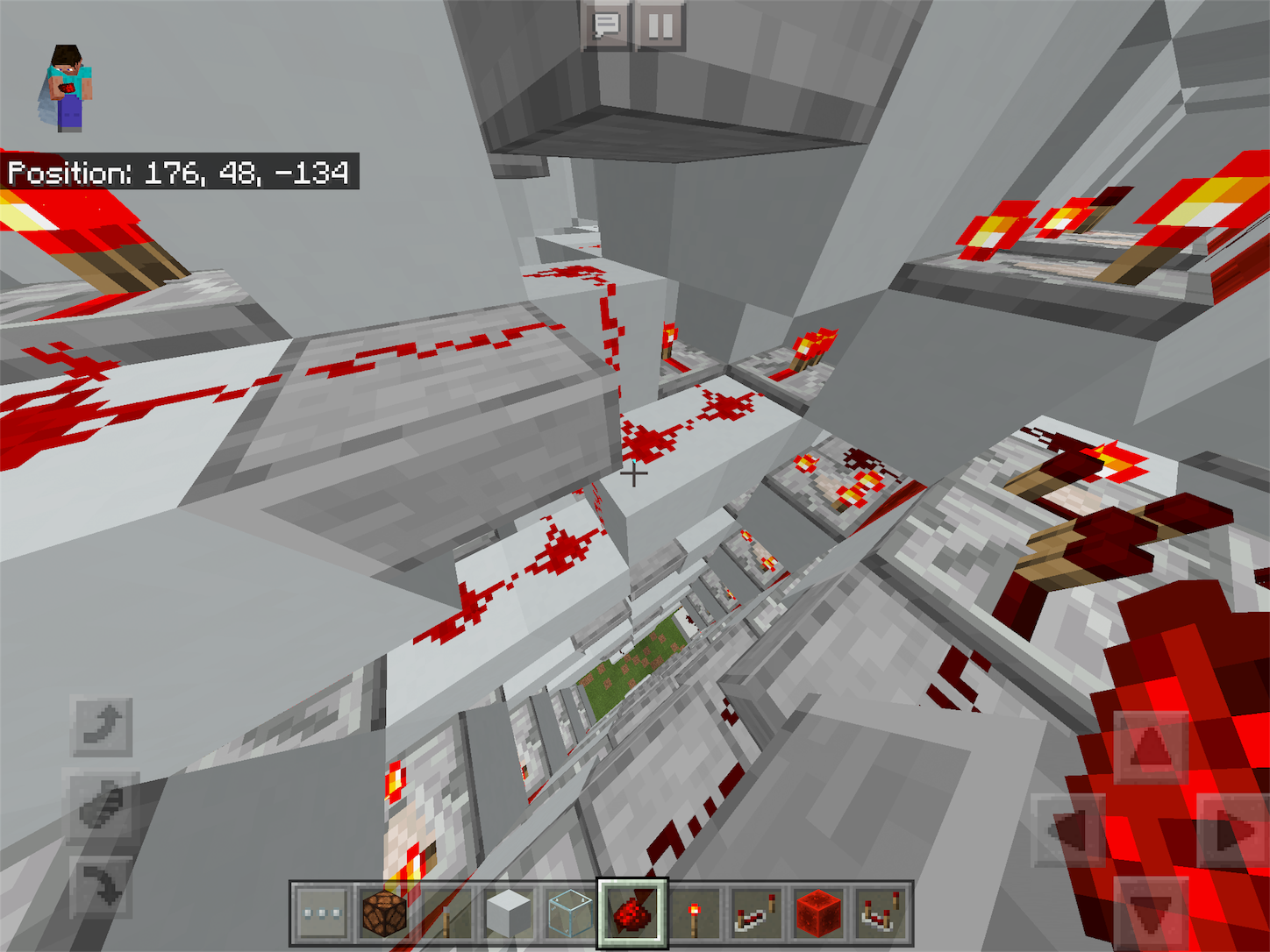
なお、最下層は減算のインクリメントを配置する必要があるので最下層の $C_1^i$ の回路は以下のようにつくる。(修正箇所は青で囲ったところのみ)

[図16]

f:id:AkaGhef:20200607154738p:image

上で解説した方法は2〜15進数の信号強度にも一般化できるが、16進数は少し仕組みが違う。

Minecraft計算機解説part1はここまでです!

この計算機は構想から実現まで2ヶ月かかってて、半加算器とかCCAの繰り上がり機構を何度も組み替えて百通り以上の組み合わせを試して見た結果、うまく乗除算に使える10進数最速(0.6tick周期)連続加算器がやっとできました。橙色の配線を見れば分かりますが強度上限15ギリギリで配線が繋がっていて、この理論上最速の計算機が存在すること自体が奇跡的な気がします(他の数十の組み合わせは多分うまくいかないので)

かなり苦しかったですが実現できた時の感動は忘れられません(´；ω；｀)

ちなみに、私はモチベが尽きたので作ってませんでしたが加算だけなら、やくみさんが16進数0.6tick周期のを実現しています。

part2は乗除算、part3はCORDICとsin計算機の解説にしようと思います。

読んで頂きありがとうございました〜ヽ('∀'*)ﾉ

赤げふの数学

数学･物理･微分の大学2年生赤げふのBLOG