Minecraft三角関数計算機報告
みなさん久しぶりです!(・ω・)ノ
あかげふです。
最近は専ら三角関数計算機にリソース全振りして制作してましたが、最新のupdateによるRender Dragonへの仕様変更により計算機開発環境を潰されたのと製作中の端末が限界を迎えつつあるので究極の三角関数計算機を作る野望は一旦損切りで打ち切りを決断しました。リソースを2ヶ月全振りしたにもかかわらずプロジェクトをお蔵入りに飛ばすのは流石に私の精神がズタズタになるので進捗報告して退去します(解決策とモチベが見つかったら帰ってくると思います)
信号強度をカラフルにするリソースパックを新versionで作成してくれる方がいたならば再開を考えようと思います。
去年2021年4月に私はCarry Cancel Adderを搭載したBEでは極小かつ最速の十進数12桁出力の加減乗除算機を制作した。そして中3からの野望であった究極的な三角関数計算機の制作に舵を切ったが、完璧主義的思考に囚われサイズの制約を厳しくしすぎた結果8月の長期休暇では完成に至らずモチベも消えたため暫く放置していた。今年2022年2月に再開を決めて、GoodNotesで設計図を詳細に書きながら計算機の構築を進めた。去年の8月に直面していた計算の技術面での困難を突破して無事に完成にいつくという三段であったが、ここからの道のりも長かった。2月末に数学物理好きの学部生が集団で宿泊して学問を語り合う数物セミナーというイベントに参加して準備等で忙しかったので数学にリソースを振っていたが、3月は本格的にMinecraftにリソースを振った。友達と3月にスキー旅行に行ったが、そのときに何度か転倒して半月板を損傷し、結局歩行に少し障害が残ることとなった。病院に診察に行くと手術をする見込みとなり、4月の中旬に全身麻酔を伴う手術をした。初めての体験であった。入院は1週間であったが、その間も痛みで夜寝られず、ストレス等で苦しみながら計算機の制作に励んだ。モチベはとうに枯渇して、数学や物理を学ぶほうが楽しいことも承知しておきながら中3からの意地を押し通すことだけで精神を突き動かして計算機の制作にのめり込んだのであった。計算機制作は設計ミスの連続で、メモリの数が1列不足したり、(パイプライン処理には回路全体の遅延を同期させておく必要があるわけだが)遅延量が合わなかったりが多発して、当初3月で終わるはずの計算機制作は4月までのびてしまったのであった。無事に退院して記事を書く今は筆者は3週間の松葉杖の生活なのであるが、ようやく慣れて健常者より歩行速度が早くなった。そんなさかな、悲劇が訪れた。1.18.30のupdateである。私は8年間BEのMinecraftをやり続けているが、Java勢と比べて計算機開発環境は決して良いものではなかった。何より時間を調整するツールが無いため、random tick rateを1000とか4000とかに引き上げることで処理を遅くして、1rstickの長さを伸ばして描画が追いつくようにして画面を録画して動作を確認するという手法を取っていた。そして私の計算機の大きな特徴である信号強度演算には、各点のワイヤーの信号強度を厳密に把握しておく必要があるため、瞬時に判断できるよう信号強度に応じて色がレインボーに変わる仕様にしてあった。このリソースパックは昔私にCarry Cancel Adderの技術を紹介してくれたYakumi氏が作成したものである。私はゲーム関連のプログラミングに疎いのでこのリソパが失効するのを恐れていた。最新のupdateにより、描画仕様が大きく変更されて現行のリソースパックは完全に使えなくなってしまった。完璧主義でかなり心を刳りながら進捗を生んでいたが、致命的な自体が起きた場合は即撤退すると決めていたので、updateの件が発覚した直後に撤退を決めた。
とまぁ経緯はこのくらいにして、技術について説明しましょうか。
Carry Cancel Adder(CCA)の仕組みについては僕の過去のblogを参照すればよい。今回は10進数演算でどのようにして三角関数を計算しようとしたかについて語る。
私の開発した10進CCA連続加算器は13桁である。三角関数を計算するにはCORDICというアルゴリズムが強力である。これは2進数の場合、事前計算したテーブルのROMとbit-shiftと加減算だけでsin,cosの計算を実現する。tanはsin/cosを除算器で求める。まず2進数でこのアルゴリズムを説明しておこう。
数3の知識を用いる。複素平面にがあったとする。点Pを反時計に原点中心で
だけ回転すると、その位置は
となる。点Qをとすると、
は
かつ
の直角三角形である。このように点Pを
だけ回転して、半直線OP方向に
倍にしてQの位置に移動する操作を便宜的に独自に「
だけ擬回転する」と呼称しよう。
であるので、「だけ擬回転する」と「
だけ擬回転する」場合で|OQ|の長さに違いがないことがわかる。「半径が擬回転の符号によらないこと」が1つめのポイントである。
とおくと擬回転で成分は
というように変化する。2進数で計算する場合、
であるとき、
は
を下位にn bit だけshiftすると求められるので乗算する必要がない。そこで、
となる
を用意しておいて、
を使って
\begin{align}\theta=\sum_{n=0}^N \varepsilon_n \theta_n\end{align}
と表せるとしよう。点(R>0)を「
擬回転」したものを点
。そして点
を
擬回転」したものを点
。...「
擬回転」したものを点
。という操作を続けざまに行うと、最終的にx軸となす角が
の点
に行き着く。この点の座標は複素数で書くと
\begin{align}\prod_{n=0}^N(1+\tan\varepsilon_n \theta_n)(R+0i)\\ =(1+\tan\varepsilon_0 \theta_0)(1+\tan\varepsilon_1 \theta_1)\cdots(1+\tan\varepsilon_N \theta_N)(R+0i)\end{align}
となる。擬回転1回はbit shiftして足すという操作だけであったので、これをN+1回合成すればの座標がわかる。
となるように
を規格化する。
\begin{align}1=|OP_N| &=|1+\tan\varepsilon_0 \theta_0| |1+\tan\varepsilon_1 \theta_1|\cdots|1+\tan\varepsilon_N \theta_N| |R+0i|\\ &=\frac{R}{\cos\theta_0\cos\theta_1\cdots \cos\theta_N}\end{align}
\begin{align}R&=\cos\theta_0\cos\theta_1\cdots \cos\theta_N\\ &=\frac{1}{\sqrt{1+\tan\theta_0^2}}\frac{1}{\sqrt{1+\tan\theta_1^2}}\cdots\frac{1}{\sqrt{1+\tan\theta_N^2}}\\ &=\frac{1}{\sqrt{(1+4^{-0})(1+4^{-1})\cdots(1+4^{-N})}}\end{align}
こうすることで、のx座標は
,
のy座標は
となる。 ここまでをまとめると、
の形で
を分解できたとき、
\begin{align}(x_{n+1},y_{n+1})=(x_n-\varepsilon_n2^{-n}y_n,y_n+\varepsilon_n2^{-n}x_n)\end{align}
という漸化式に従うとを得る。
あとはという分解の仕方を考えればよい。
という近似をすれば、
となる。
つまり2進数と同様の分解の仕方で考えることができる(この事の正当性については後で挙げる記事を参照してほしい)
の符号を
として、
の符号を
として、
...、
の符号を
とすればよい。
なお一般のに対し
であるが、
打ち切り誤差を発生させてとする。
この話を10進数化して考える。
擬回転で変化する成分はとなって、これが計算しやすいように2進数の場合は「
」となるように選んだのであった。安直に
として考えてみる。CORDICのポイントである「擬回転したあとの半径は符号(回転が時計か反時計か)によらない」ことから、
という形の分解を考えることになる。という近似で考えてみるとわかるが、つねに
となる
が存在するとは限らない。結論を言うと、分解の仕方は次のようになる。
このような分解の仕方に至った考え方や、定義域内のに対して
のかたちの分解
が存在すること、そして再帰的に分解できることは自明ではないが、私のmathlogの記事に書いた。
\begin{align}R&=\cos\theta_0\cos\theta_1\cdots \cos\theta_N\\ &=\frac{1}{\sqrt{1+\tan\theta_0^2}}\frac{1}{\sqrt{1+\tan\theta_1^2}}\cdots\frac{1}{\sqrt{1+\tan\theta_N^2}}\\ &=\frac{1}{\sqrt{1+10^{-2×0}}}\frac{1}{\sqrt{1+1^2×10^{-2×1}}}\frac{1}{\sqrt{1+2^2×10^{-2×1}}}\frac{1}{\sqrt{1+2^2×10^{-2×1}}}\frac{1}{\sqrt{1+4^2×10^{-2×1}}}\cdots\frac{1}{\sqrt{1+4^2×10^{-2M}}}\end{align}
擬回転の成分変化は
\begin{align}(x_{n+1},y_{n+1})=(x_n-\varepsilon_n\dfrac {c_t}{10^{s+1}}y_n,y_n+\varepsilon_n\frac {c_t}{10^{s+1}}x_n)\end{align}
となる。は掛け算を行うのではなく、
を足し引きすると考える。
こうすることで10進数でCORDICを行うことができ、加減乗除とシフト(で計算を実行できる。ROMに記憶させる必要があるのは事前に計算した
の値である。
以上が僕が独自に10進数用に改変したCORDICアルゴリズムであるが、Minecraftで究極的な計算機を作るためにはさらに工夫を要した。その結果制御配線が複雑になった。そのゴミのような回路群を解説する気はないが、本質的なアイデアについては説明しようと思う。そもそもMinecraftでは計算機に使いやすいROM、特に10進数計算なので信号強度を所定のタイミングで引き出せるROMは構造が限られてくるし、10進数1桁あたりの大きさは3.75×2×2ブロックである。なので記憶する数を増やすと列数が増えて制御配線が大きくなるし、サイズも大きくなる。制御配線を増やしてでも記憶素子の数を減らすことが重要である。繰り上がり無遅延でとどく最大のCCAは13桁で、下位2,3桁は誤差として棄却するとした。度数法での計算で、入力は上位2桁が整数、下位11桁が小数部、出力は上位1桁が整数部とした。なので結果の打切り誤差や累積する加算の誤差は、
の誤差は
程度になるように調整した。
私が製作中だった計算機では
という分解の過程を3段階に分割して極力記憶素子の量をへらすようにした。
最初は通常のCORDICどおりのアルゴリズムで計算する。
次にn>N/3のときは段階が変わる。
をテイラー近似すると
となる。
程度であれば
という線形近似で十分である。だからN/3に近い4で割ると1あまる整数Kをもってくると
のときは
を下位にシフトして
倍すると得られる。
さらにn>N/2のときは段階が変わる。
擬回転の成分変化ではx,y成分のシフトを行うが、シフトではみ出した分は加算器の桁数からはみでるので捨てられる。n>N/2のときシフトする数は加算器の桁数の半分以上なので、2度同じ桁数をシフトすると加算器上では丸め誤差で0になる。このことから擬回転による成分変化の漸化式を簡約化することができる。L=N/2=2Mとするとn>Lのとき
\begin{align}(x_{n+1},y_{n+1})=(x_n-\varepsilon_n\dfrac {c_t}{10^{s+1}}y_n,y_n+\varepsilon_n\frac {c_t}{10^{s+1}}x_n)\end{align}
という漸化式は
\begin{align}(x_{n+1},y_{n+1})=(x_n-\varepsilon_n\dfrac {c_t}{10^{s+1}}y_L,y_n+\varepsilon_n\frac {c_t}{10^{s+1}}x_L)\end{align}
となる。計算機の内部構造に関する話をすると、中にはCCAの連続加算器が搭載されているので加算を次々行うことはできるが、シフトはできないので一旦値を取り出してシフトレジスタでシフトするステップがあるのでシフト数が増えると遅延量が増える。この近似を行うことにより、シフトさせるのはという量なのでいちいち加算器から値を取り出す必要がなく、高速化につながる。さらに私の前回の乗除算機の仕組みを見て類推してもらうと、第3段階は乗除算の構造と全く同じとなる。適切に近似を行った結果、第3段階はCORDICのアルゴリズムの手続きからは外れたものとなった。
の部分剰余を
で回復型除算で割った結果で得られる符号をダイレクトに
(をシフトしたもの)の足し引きの符号につなげる。
幾何的に見ると、第3段階では擬回転の角度の変化が微小なので原点中心の円に接する方向の直線上での移動とみなすことで線形近似を行うことに対応する。線形近似なので比率の計算として乗除算器の構造を応用したということである。
第3段階は複雑なのでもう少し乗除算器との対応を丁寧に説明すべきであるが、忙しいのでややテキトーに済ませる。
数式的にみると、入力を大小の角度に分割
して
[tex:\sin\theta=\sin \theta_{big}\cos \theta_{small} +\cos \theta_{big}\sin \theta_{small} = \sin \theta_{big} +\cos \theta_{big} \theta_{small}]
という線形近似を行ってbig,smallの計算をそれぞれ第1,2段階と第3段階にて行ったものと解釈できる。
そしてこれらの計算をパイプライン化された1個のCCA内部で同時にこなす技術について説明しようと思う(続きはまたこんど書く)
あとtanの計算もただの除算器であるが、パイプライン処理の割当について述べて、全体の符号の処理方法、自動補数反転機能によるθの自動分解についても詳しく解説したい。
ここまで読んでいただいてありがとうございます。
RenderDragonでリソースパックが死んでしまいましたが、もし信号強度を見やすくするリソースパックを開発してくださる方がいれば一報お願いします。
しばらくはMinecraftからは距離を置こうと思います。(計算機の制作方法に関するアドバイスや質問は快く回答するのでぜひ)
Minecraft界隈の人好きです。界隈の技術勢オタクたちはこれからも頑張ってください。
また会えたらMinecrafterとして会いましょう。
2020 学園祭 発表資料
こんにちは(*^^*)
バーゼル問題の初等幾何的証明のGeogebraツールを使用したスライドのリンクを置いておきます。
https://www.geogebra.org/m/wqjxctwc
左上のスライダーを右に移動させるとスライドを切り替え、
そして左上のスライダーを1番右にした上で、左下のスライダーを右に移動させると分裂の様子が見れます。右下のスライダーを移動させるとライトを分裂させられます。
D^(2)型Affine Geometric Crystal
こんにちはヽ(^0^)ノ
https://arxiv.org/pdf/math/0512657.pdf
アフィン型幾何結晶(geometric crystal)のこの論文を読んでいたら、微分作用素表示が出せそうと思ったので計算したら公式を発見・導出できたので紹介します。今回は型です。
論文にある写像は幾何結晶として要請からリー群の作用とみなせてパラメータ微分の計算をタラタラすると得られました。derivative representationと言う名前を見かけたので使っていますが、この対象を微分作用素の環の元として表示するモチベはあまり無いっぽいですね(?)
\begin{align}e_0=\dfrac{x_0^2-x_1y_1}{x_0^2+x_1y_1}x_0 \dfrac{\partial}{\partial x_0} -\dfrac{2x_1y_1}{x_0^2+x_1y_1}\left(x_n \dfrac{\partial}{\partial x_n}+\sum_{k=1}^{n-1}x_k\dfrac{\partial}{\partial x_k}+y_k\dfrac{\partial}{\partial y_k}\right)\end{align}
\begin{align}e_i=\dfrac{y_i}{x_iy_i+x_{i+1}y_{i+1}}\left(x_i^2\dfrac{\partial}{\partial x_i}+x_{i+1}y_{i+1}\dfrac{\partial}{\partial y_i}\right)\ \ \ \ (1≦i≦n-2)\end{align}
\begin{align}e_{n-1}=\dfrac{y_{n-1}}{x_{n-1}y_{n-1}+x_n^2}\left(x_{n-1}^2\dfrac{\partial}{\partial x_{n-1}}+x_n^2\dfrac{\partial}{\partial y_{n-1}}\right)\end{align}
\begin{align}e_n=x_n\dfrac{\partial}{\partial x_n}\end{align}
型Cartan行列
\begin{align}a_{ij}=2\ \ \ i=j\end{align}
\begin{align}a_{ij}= -2 \ \ \ (i,j)=(0,1),(n,n-1)\end{align}
\begin{align}a_{ij}=-1 \ \ \ |i-j|=1かつ(i,j)≠(0,1),(n,n-1)\end{align}
\begin{align}a_{ij}=0\ \ \ \rm{otherwise} \end{align}
このとき次のVerma関係式が成立する
\begin{align}a_{ij}=0⇒c^{e_i}d^{e_j}=d^{e_j}c^{e_i}\end{align}
\begin{align}a_{ij}=-1⇒c^{e_i}(cd)^{e_j}d^{e_i}=d^{e_j}(cd)^{e_i}c^{e_j}\end{align}
\begin{align}a_{ij}=-2⇒c^{e_i} (c^2d)^{e_j} (cd)^{e_i} d^{e_j}=d^{e_j} (cd)^{e_i} (c^2d)^{e_j} c^{e_i}\end{align}
次の等式も要請されます
\begin{align}c^{e_m}d^{e_m}=(cd)^{e_m}\end{align}
の作用は以下の通りです。
、
、
、
\begin{align}c^{e_0}・f=f\dbinom{x_0cT_0,x_1T_0,x_2T_0\ldots,x_{n-1}T_0,x_nT_0}{y_1T_0^{-1},y_2T_0^{-1},\ldots,y_{n-1}T_0^{-1}}\end{align}
\begin{align}c^{e_i}・f=f\dbinom{x_0,x_1,\ldots,x_iT_i,\ldots,x_n}{y_1,\ldots,y_{i}cT_i^{-1},\ldots,y_{n-1}}\end{align}
\begin{align}c^{e_{n-1}}・f=f\dbinom{x_0,x_1,\ldots,x_{n-1}T_{n-1},x_n}{y_1,\ldots,y_{n-1}cT_{n-1}^{-1}}\end{align}
\begin{align}c^{e_n}・f=f\dbinom{x_0,x_1,\ldots,x_{n-1},cx_n}{y_1,\ldots,y_{n-1}}\end{align}
前回と記事の構成ほぼ同じですゴメンなさい(Dynkin図形似てるので)
C_n^1型アフィン幾何結晶の微分作用素表示
こんにちはヽ(^0^)ノ
https://arxiv.org/pdf/math/0512657.pdf
アフィン型幾何結晶(geometric crystal)のこの論文を読んでいたら、微分作用素表示が出せそうと思ったので計算したら公式を発見・導出できたので紹介します。今回は型です。
論文にある写像は幾何結晶として要請からリー群の作用とみなせてパラメータ微分の計算をタラタラすると得られました。derivative representationと言う名前を見かけたので使っていますが、この対象を微分作用素の環の元として表示するモチベはあまり無いっぽいですね(?)
\begin{align}e_0=\dfrac{x_0-x_1y_1}{x_0+x_1y_1}x_0 \dfrac{\partial}{\partial x_0} -\dfrac{x_1y_1}{x_0+x_1y_1}\left(2x_n \dfrac{\partial}{\partial x_n}+\sum_{k=1}^{n-1}x_k\dfrac{\partial}{\partial x_k}+y_k\dfrac{\partial}{\partial y_k}\right)\end{align}
\begin{align}e_i=\dfrac{y_i}{x_iy_i+x_{i+1}y_{i+1}}\left(x_i^2\dfrac{\partial}{\partial x_i}+x_{i+1}y_{i+1}\dfrac{\partial}{\partial y_i}\right)\ \ \ \ (1≦i≦n-2)\end{align}
\begin{align}e_{n-1}=\dfrac{y_{n-1}}{x_{n-1}y_{n-1}+x_n}\left(x_{n-1}^2\dfrac{\partial}{\partial x_{n-1}}+x_n\dfrac{\partial}{\partial y_{n-1}}\right)\end{align}
\begin{align}e_n=x_n\dfrac{\partial}{\partial x_n}\end{align}型Cartan行列
\begin{align}a_{ij}=2\ \ \ i=j\end{align}
\begin{align}a_{ij}= -2 \ \ \ (i,j)=(1,0),(n-1,n)\end{align}
\begin{align}a_{ij}=-1 \ \ \ |i-j|=1かつ(i,j)≠(1,0),(n-1,n)\end{align}
\begin{align}a_{ij}=0\ \ \ \rm{otherwise} \end{align}
このとき次のVerma関係式が成立する
\begin{align}a_{ij}=0⇒c^{e_i}d^{e_j}=d^{e_j}c^{e_i}\end{align}
\begin{align}a_{ij}=-1⇒c^{e_i}(cd)^{e_j}d^{e_i}=d^{e_j}(cd)^{e_i}c^{e_j}\end{align}
\begin{align}a_{ij}=-2⇒c^{e_i} (c^2d)^{e_j} (cd)^{e_i} d^{e_j}=d^{e_j} (cd)^{e_i} (c^2d)^{e_j} c^{e_i}\end{align}
次の等式も要請されます
\begin{align}c^{e_m}d^{e_m}=(cd)^{e_m}\end{align}
このような系があります。
\begin{align}φ(x):=\dfrac{z}{yz+x}\left(y^2\dfrac{\partial}{\partial y}+x\dfrac{\partial}{\partial z}\right),c,d∈ℂ^×\end{align}
\begin{align}c^{φ(d^{-1})}d^{φ(c)}=d^{φ(c^{-1})}c^{φ(d)}=(cd)^{φ(1)}\end{align}
Minecraft Redstone D-CCA Multiple&Division(part2)
こんにちはヽ(^0^)ノ
この記事はpart1の続きなので、読んでなければ先ずpart1から見て欲しいです。
乗除算について解説していきます。
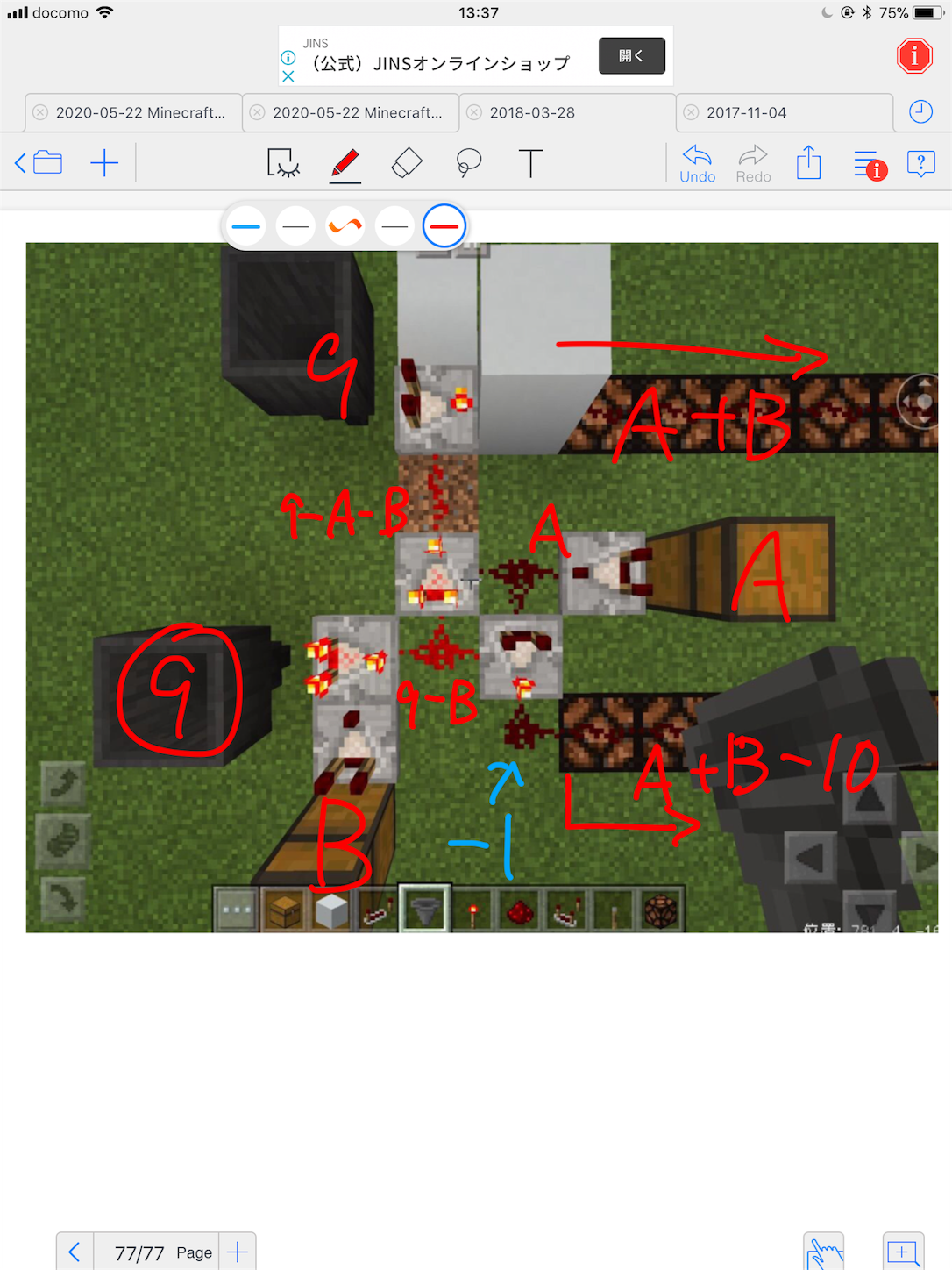
この連続加算器は6tick周期でパイプライン演算をしているので時刻毎に割り当てられた6個の連続加算を同時並行でできるが、乗除算を行う際はそのうち2区画を使っておこなう(工夫すれば3個同時並行でできる)。
以後tickはrstickのことを指すとする。
昔私は乗除算をこのDCCA(decimal carry cancel adder)上で同じ手法でできる方法を思いついたので解説する。DCCAの桁数は上限の13桁が出力の限界だが、理論上最大誤差が50(最下位桁が1の位として)出るので出力の有効数字は11桁であるが、平均的な誤差は10程度で済む。
この計算機では小数点の位置をあまり自由に動かすことが出来ないため、入出力の形式は
、有効数字
桁
先ず除算について見るが、手順は筆算ベースであり、
を例に取って見ていく(ちなみに
はベルヌーイ数)

中段のなどの数字は部分剰余と言い、無限小数である場合は部分剰余を割る操作を永遠と繰り返すことになるが、計算機は途中で打ち切る。簡単の為に加算器は13桁ではなく6桁とし、小数点は無視する。
は部分剰余で初期値は被除数
、Bを除数
(をシフトしたもの)、
は商をカウントするためのインクリメント[デクリメント]の
であり、
は(暫定的な)商で、初期値は
ある。筆算と少し違う点が、次の段の部分剰余を求める際に
から
を引くのでは無く、
から
を何回か引いて行う点であり、乗算を使わずに済み、
の値を見積もる必要が無い。
を引く度に
を足すことで商をカウントしている。これを繰り返し
から
を引きすぎたら一旦
を
に足して修正して、
を引いてカウントをバックしている。これで次の段の部分剰余が求まるので、
を1つシフトダウンしてまた次の段の部分剰余を求める操作を行う。ループは以下の手順。
(1)AからBを負の数になるまで0~9回引く(赤線)
(2)引く毎にに
を足し、商をカウント(赤線)
(3)Aが負の値になったらを足す(緑線)
(4)を引き、カウントをバック(緑線)
(5)を1つシフトダウン(青線)

次に乗算について、
を例にとって見ていく。
[筆算]

3つの数を同時に足しあげるのは計算機的に困難なので2数ずつ足しあげる筆算の書き方をしているが、雰囲気は掴んで貰えるだろう。途中で出てくるの数字の段(緑矢印)を部分和と呼び、除算同様に小数点は無視する。
は乗ずる回数の書かれた数で初期値は乗数
、
は被乗数
(をシフトしたもの)、
は乗ずる回数を
からカウントダウンするためのインクリメント[デクリメント]の
である。
は部分和の役割で、最終的に積
の答えとなる。
を引いてカウントダウンし同時に
を加える操作を
が負になるまで行う。
が負になるとカウントし過ぎなので
を加え、
を引き修正する。これで部分和が求まったので次の段の部分和を求める為に
を1つシフトダウンする。ループをまとめると以下のようになる:
(1)を負になるまで引く(赤線)
(2)引くごとにを足す(赤線)
(3)が負の値になったら
を足す(緑線)
(4)を引く(緑線)
(5)を1つシフトダウン(青線)
[表]

乗除算の類似性と実際の回路の手順について説明していく。図や、乗除算それぞれで示したループの手順を見るとほぼを入れ替えただけで、処理内容がとても似ていることが分かる。そこで連続加算器がパイプライン処理であったことを巧妙に使って、
計算機のコア内に入っているにタイミングよく
を入力することで乗算と除算を使い分けることが出来る。加算器は6tick周期なのでそれと同期できるように
を保存する外部のメモリは6tick周期で巡回するコンパレータの構造となる。
パイプライン処理で同時に3個の乗除算を行えるが本解説では1個の乗除算のみに限定し更に高速化を試みる。先程ループの手順を示したが(5)のをシフトダウンする際、6tick周期のメモリの場合
シフトする部分に信号が回ってくるまで待つ必要があるためシフトダウンする部分で遅延が生じて、[表]での緑,青の部分の処理をした後の赤の部分の処理に入力が間に合わない。そこでメモリを2tick周期にしてみると、連続加算器の周期が6tickで、2tickはその約数となっているため、2つのスロットにを入れておくと問題なく処理できる。そして
が奇数時刻か偶数時刻にコアに入力されるかどうかで乗算と除算を切り替えられる。(これを閃いた時はまさに最適解だったのでめちゃ嬉しかった)
制御回路で実際に動かしていく方法を見る。今手元に制御回路が完成された乗除算器が無く、申し訳ないが忙しいせいで載せることが出来ない。

前回補数の項目で話をしたように、減算結果が負であるかどうかは、減算したときに最上位の繰り上がり出力(以後と書く)が
ならば結果は0以上である。乗算の場合
の減算をしたとき
ならば減算結果が
以上なので次は赤色の矢印の操作を行い、減算か加算かを制御する(J)の配線をonにして次も減算を行う。逆に
のとき減算結果が負なので青,緑の矢印の操作を行う、すなわち(J)の信号をoffにし次は加算モードにして、(K)に信号を送って
を1つシフトダウンする。また除算の場合は、上記の
を
に読み替えると全く同様の処理であることが理解出来る。
((J)に信号を送る部分を最小遅延で行える回路の実現がかなり大変で2ヶ月も苦労したんですよね)
以上の手続きをアセンブリ風に書いてみる(だいぶ前に書いたものなので正当性怪しいのでお気持ち程度に...)
アセンブリは、デカい命令が書いてある主記憶装置、演算を行う部分、演算結果を記憶する部分(以下Acc)、の3つに分かれる。命令はadd・subで番地指定した所の値をAccに加えたり引いたり
基本番地が低い所から命令を実行していく。
loadは指定した番地から値を引き出し、Accに上書き。
atoreは指定した番地にAccの値を上書き。
jumpは指定した番地から処理を始める。
jump minusはAccの値が負ならjumpと同じことをする。
本当は無いが、面倒なのでmultipleとdivideという命令を追加し、それぞれ掛ける、割る の命令とした。

最後まで見て頂きありがとうございますm(*_ _)m
記事は2週間前に完成してたのですが、アップロードエラーを吐かれてやる気を失って遅くなりました。
暫定的ではありますが、高3の身分ゆえ冠模試があるので受験勉強に集中したいと思いますまる
sin計算機の解説も未定です。。。
それでは〜〜
Minecraft Redstone Decimal Carry Cancel Adder(part1)
こんにちはー(・ω・*)ノノ
計算機を制作していたのですが、cloneミスで計算機が吹っ飛んだり度重なるクラッシュで戦意喪失したので解説を投げて私の受験が終わるまで制作を中断しようと思います(;´д`)
基礎的な論理回路と2進数の加算器は既知として説明しますが、他何か不詳な点あれば説明を足すので指摘ください!
作り方は最後の方にあります。
タイトルのCarry Cancel Adder(CCA)とは外国人のMajic氏が開発した2進数加算器(binary adder)であり、2進数14bitの加算が繰り上がり(carry)の遅延が無いという凄すぎる技術を天才すぎるアイデアで実現したものである。元動画リンク:
しかし、5年経った今でも知名度が低いのが現状である。私は丁度3年前にこの2進数の加算器を10進数の連続加算器(decimal loop adder)にかなり時間をかけて改良し、加算を何回も出来るようにした。CCA(Carry Cancel Adder)の説明をした後、連続加算器があれば乗除算を高速かつ同じマシンで出来るようになる方法があるので紹介したい次第である。最終的には三角関数計算機の解説を目標とする。便宜上数式を使うが、実際の理解としては感覚に近いと思う。
信号強度半加算器
信号強度加算器では信号強度とデータの値を対応させて、コンパレータの減算モードを何個か用いて計算するもので、2進数と半加算器が2つ並んで全加算器を構成し、全加算器が加算器を構成していることと似ている。
コンパレータ減算モードの挙動は、背面,側面の入力,出力をそれぞれとして
と表される。
ここではRamp関数であり
の整数の加算について見ていく。
のとき
となるが、値の範囲を確かめれば
となることが確認出来ると思う。
のとき1の位の値は
なので
で表せる。2つの数式を見比べると、共通して
という部分が含まれているので、ここから回路を小型化できそうだと私は昔閃いた。
の形をコンパレータ減算モードだと思えば、数式に従って次のように回路が実現できる。(-1は強度1減衰と考える)
[図2]
この回路は下位からの繰り上がりを考慮していないので半加算器と呼ぶ。2進数の場合は半加算器を2つ並べて、ある桁の入力,下位からの入力
からその桁の出力
,上位桁への繰り上がり出力
を出力する全加算器を構成している。10進数の場合は全加算器は半加算器1つと、
を考えた
の操作をする部分に分かれる。
CCA 繰り上がり計算機構
ここからがCCAの枢要たる部分だが、桁程度の加算では全ての
を各桁の
から瞬時に計算できるのである。加算の筆算では下位桁から順に計算するように、加算する桁数に比例して計算に時間がかかるので、全体の計算時間のネックとなるのでここを高速化する必要がある。アイデアは冒頭で挙げたリンク先から得たもので、加算器の理論を後から知ったのでそれを加えて解説していこうと思う。下位から第
桁目の
値をそれぞれ
と書く。
現実の々加算器には高速化の手段としてCarry Look Aheadがありその中にPG信号という理論がある。繰り上がりがどう上位の桁に影響を及ぼすかを見るために、各桁について"propagate"か"generate"という概念を定める。進法(
で十分)の加算で、
であるとき、第
桁はpropagate状態、(P)という。また、
のとき、generate状態、(G)という。本解説では便宜をはかって、(P)でも(G)でもないとき、cancel状態、(Cc)と呼ぶことにする。(P)、(G)、(Cc)は排反(2つが同時に起こり得ることは無い)で、いずれかひとつの状態である。足し算の筆算を書きまくって確かめて欲しいが、具体例を1つ書いた。
[図4]
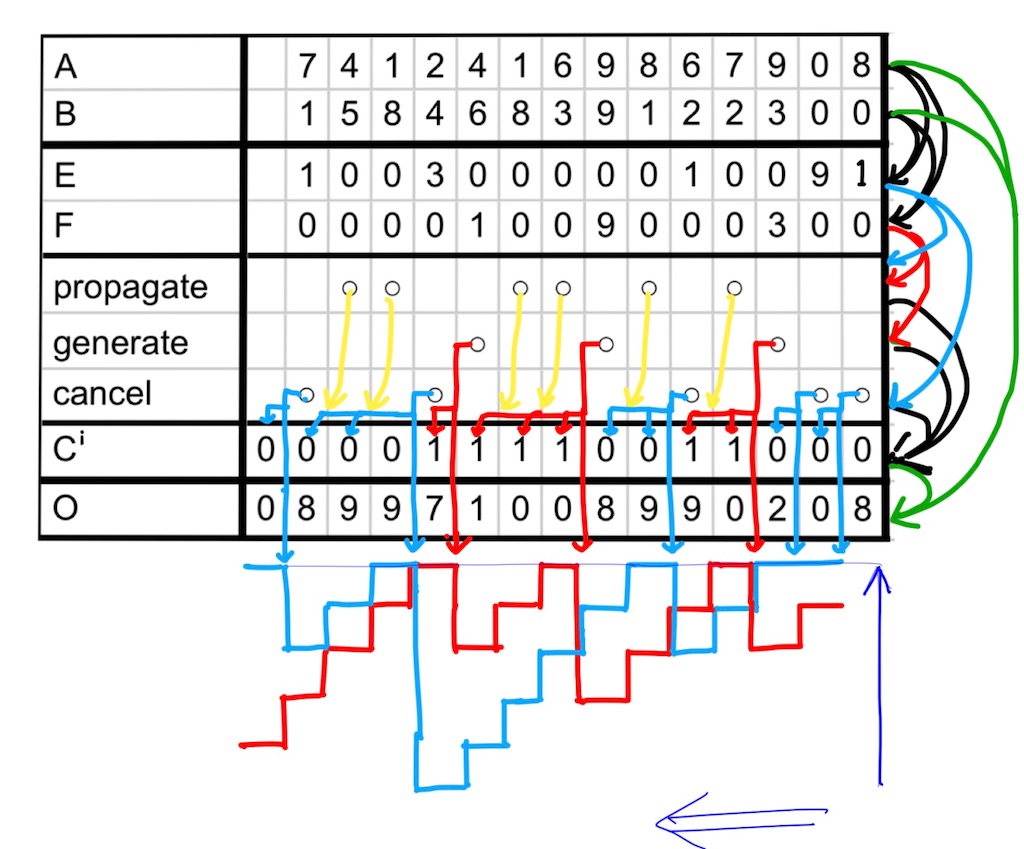
CCAでは2本の信号強度の配線の強度の大小関係でを決定しており、ワイヤーと大小関係を比較するコンパレータしかいらないので上位桁にもほぼ遅延無く情報が届き即座に
の決定ができる。第
桁が(P)であるとき
が成り立つが、まさに第
桁の繰り上がり出力が第
桁をそのまま伝搬(propagate)し、第
桁に入力されている。(G)は繰り上がりが発生(generate)すること意味し、(P)が続く限り伝搬し続ける。ここまでは現実の理論体型と同じだが、繰り上がりが発生しない(Cc)のときは「(P)が続く限り繰り上がりを阻止(cancel)する波が伝搬する」と捉えることで2本目の信号強度配線を導入したのである(私はそれまで1本だったので驚いた)。マイクラで回路を作成する際、(P)の伝搬は上位への一方通行であることに注意して、下の[図6]のように半blockを使って整流して下位に信号が流れないようにする(開発者の発想が天才すぎて泣く)
[図4]のように階段状の図を描き、(G)側の赤色のグラフと、(Cc)側の水色のグラフを規則に従って書いている。赤色のが水色より上側のときで、逆ならば
である。グラフの縦軸は信号強度を指し示しており、強度の大小関係をコンパレータで決定して
を出力する。グラフの規則は、(G)があったときは赤色を上限値まで上げて、(Cc)があったときは水色を上限まで上げる。(P)であるとき(黄色矢印)は信号強度配線には何もせず、赤色と水色両方を1段階減衰させるが、大小関係は保存されている。
以上が決定の流れである。半加算器をベースに、(P)、(G)、(Cc)のどれであるかを決定する回路を見ていく。
、
としたときに、
となることを[図4]を見て確かめてみてほしい。
1以上か0であるかはリピーターやトーチで簡単に判定できるし、(P)はNOR回路である。CCAの機構をを用いて回路にするとこうなる。
[図6]


信号強度全加算器
最後のステップである加算結果を出力する回路について見てく。
は(Cc)のときの加算結果を計算する回路に使える、つまり繰り上がり入力を
としたとき
である。は(G)のときの加算結果を計算する回路に使える、つまり
(P)のときはめんどくさいことが起きる。k桁目が(P)のとき半加算器の出力はで、
ならば
だが
ならば
となるので、信号強度に
を足し引きして
を計算するわけには行かない。だから別途配線を用意する必要がある。
[図8]
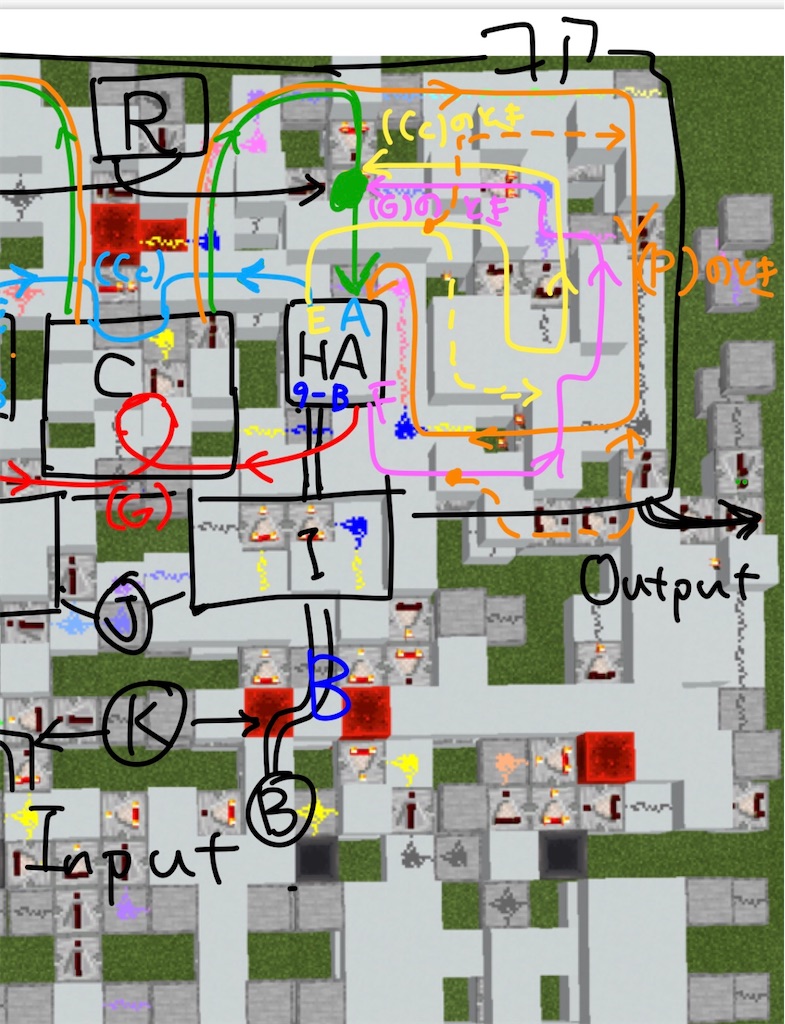
実際のマイクラの回路は上のようになる。(めんどくさいので)連続加算器の画像をそのまま使っているが、加算器も連続加算器も仕組みはほぼ同じで、加算結果がそのまま
に繋がれて代入されているという違いだけである。[HA]は半加算器、[C]はCCAの繰り上がりの計算機構、Bが入力、[R]はリセットの配線、[I]は
を
にする回路で、桁毎に何層も積み重なっている計算機の1桁分(2マス)だけ切り出してきた断面の画像である。さっきの[HA]でE,Fを計算し、(G)の繰り上がり計算部分は[図4]の階段のグラフの赤色と同じで、信号強度配線に繋がっている。(Cc)の繰り上がり計算のための信号強度配線は同じように水色である。(G)のときの加算結果はピンク色で、(Cc)のときは黄色、(P)のときは橙色の矢印で書いている。黄色破線は、
どちらの値を半加算器の出力として使うかを決定するものである。
[図8]の橙色破線は、(P)の時のを出力する部分の
からの入力で、
のときは
を出力するようになっている。[C]の部分から
が出力され、(P)以外のときは水色の丸の部分で半加算器の値と
から
を計算している。[R]はリセットの配線で、Aの値を0にするが、ここの部分の回路だけ非同期なのでパイプライン処理出来ない。
パイプライン演算
パイプライン演算は計算機においてかなり重要な概念であるのでここで説明しておきたい。ループ式の計算回路で、信号を回路内で何周もさせて計算する際、信号の辿るルートによって遅延が異なる場合は周回する毎に遅延が拡大していき周回するうちに1周回遅れて前の信号と干渉してしまう。このためループ計算の回路において、「信号が回路を1周回して戻るときの遅延量は経路によらず等しい」という強い条件「同期」が必要となる。ここではループ計算において同期を定義したが、一般に信号の入力から出力までの遅延量が経路によらず等しければ同期式回路である。
同期式のループ回路において時刻毎に処理が独立していて、1rstick毎に違う信号を入力したとき何個もの計算をほぼ同時にやることが可能で、これをパイプライン処理と言う。信号が波形を崩さずに配線を伝搬していく様子が波に見えることから特にウェーブパイプラインと呼ばれる。マイクラの場合で注意すべきだが、遅延2のリピーターに1rstickパルスが入力された時に2rstickのパルスが出力されて前の時刻の信号と干渉してしまうため1tick毎に違う処理を行う際は2rstick遅延のリピーターは使用できないという制約が追加される。ウェーブ型以外もあって、遅延量が一定でない場合一旦バッファという領域に信号を保存し回路全体の時刻調整をする"クロック"の制御のもとで同時に情報を次の処理領域に渡したりする。
補数による減算
減算は補数の概念を使えば驚くほど楽に加算器上に実現できることが知られている。今回は信号強度加算器が主題なので、10進数N桁の整数の補数の計算から減算
を行う方法を考える。まず答えが正になる場合について見ることにし、
の位を
と書くと
と表せる。
とし、さらに
と定義する。
の補数とは
であり簡単な計算から
と分かる。
となり、下位
桁には影響が及ばないので
を無視すると、
という「足し算」を計算すればいいことになる。ここで
から
を求めるには各桁で独立に
から
を求めればいいので、すぐに求められる。
また、の部分は加算器の最下位桁の繰り上がり入力
が空いているので、ここから入力すれば良い(インクリメントをここで使うのか!と、最初知ったときは仰天した)
この加算を行うと、無視したの分があるので答えが正のとき必ず最上位桁の繰り上がりが起こる(
)
e.g.)
逆に減算結果が負ならば最上位桁の繰り上がりが起こらずとなるので、負になったかどうか判別できる。しかし減算結果の数字を出力するには絶対値を出力しなければならないので、加算結果の補数を見る必要がある(丁寧な説明が困難なので具体的な計算手順をみて掴んでください)
e.g.)
一応数式を載せると、
しかし減算器単体として運用する場合は、加算結果の補数を求める際に+1(インクリメント)をしなければならず面倒なので連続加算器であることを利用した2つの解決方法を述べる。を
の補数反転と呼ぶことにする(元々補数は2進数の概念で、補数を求める時は各桁でNOTゲートを通す、つまりbit反転すればよい)
ひとまず+1なしで加算を計算しの加算で
ならば+1をして出力、
ならば
補数反転を計算して出力する()
連続加算器なのでオーバーフローしなければ連続減算も可能で、引く時は減数の補数を加えると良いが、第2の方法としては総和結果が負になる場合、1を引く、すなわち補数であるを加えてから、出力を補数反転させてやると絶対値が出る
e.g.)
私の計算機は当初から乗除算を前提として設計された為、加減算を同じマシンでできるようにしている。と
は補数にしてから足すかの違いなので、1つの入力で切り替えられるようにしている。それが[図8]における[I]の役割であり、(J)の部分で加算か減算かを制御している。(J)がonなら減算するモードになる。
最後に連続加算器全体の構造と作り方を見ていく。[図8]では少し説明を端折ったが[図12]のように加算器は下位桁から上位桁に向かって下側から左右交互ジグザグに桁が配置されていて(偶数桁目は右側という感じで)、CCAの機構を最大限活かして限界である10進数13桁(14もギリギリ)の構成になっている。ただこの加算器を2個上下に重ねて下側の加算器の最上位の繰り上がりのところを上側の加算器の最下位桁の繰り上がり入力に繋げれば2倍の桁数の加算器が作れる。また、交互に重ねずに2highずつ重ねていくと高さは半分で桁数が半分の7桁、横の長さが半分の連続加算器も作れる(ちと時間が無くて作れないので今は画像が無い )
[K]は入力Bをコア内に入力するかどうか決める配線で、[M]はシフトレジスタ(メモリ)、[S]はシフトする部分
出力する機構が少し面倒で、信号が内部を流れているのでF側の配線から信号取り出す必要がある。
に
を代入する、または
の状態で(J)をonにすると補数反転されて
が代入される。そうすると[図8]のようにピンク色の配線に
の強度の信号が流れるので、[output]と書いた部分から信号を取り出す。
[図10]

[図12]

各層は2highの厚さで、左右交互に桁が積み重なっているので、線対称な直線で切った[図14]を左右交互に積み重ねるようにして、cloneコマンドを実行すると13桁の計算機が出来上がる。1桁分に必要な回路の部分は[図8]の仕組みを理解していれば分かるだろう。
赤色の部分は乗除機を作る上で上から下に信号を送る必要があるのでそこの部分だけは螺旋状にワイヤーを設置する([図15]参照)
[図14]

[図15]
なお、最下層は減算のインクリメントを配置する必要があるので最下層のの回路は以下のようにつくる。(修正箇所は青で囲ったところのみ)
[図16]

上で解説した方法は2〜15進数の信号強度にも一般化できるが、16進数は少し仕組みが違う。
Minecraft計算機解説part1はここまでです!
この計算機は構想から実現まで2ヶ月かかってて、半加算器とかCCAの繰り上がり機構を何度も組み替えて百通り以上の組み合わせを試して見た結果、うまく乗除算に使える10進数最速(0.6tick周期)連続加算器がやっとできました。橙色の配線を見れば分かりますが強度上限15ギリギリで配線が繋がっていて、この理論上最速の計算機が存在すること自体が奇跡的な気がします(他の数十の組み合わせは多分うまくいかないので)
かなり苦しかったですが実現できた時の感動は忘れられません(´;ω;`)
ちなみに、私はモチベが尽きたので作ってませんでしたが加算だけなら、やくみさんが16進数0.6tick周期のを実現しています。
part2は乗除算、part3はCORDICとsin計算機の解説にしようと思います。
読んで頂きありがとうございました〜ヽ('∀'*)ノ
Kac-Moody代数の疑問
こんにちは
自分でもまだ整理が済んでない部分がありますが、自分の思いついた概念(多分既出)がどう出てくるのか知りたいので書きました
Kac-Moody代数:

Weyl代数:]
Weyl代数を以下のように表されるもの全体の集合とする:
が成立するが
より、
と同一視できる。すなわち
と書ける。Kac-Moody代数をの生成元がある行列と対応するが、この同一視によってWeyl代数の元にKac-Moody代数を埋め込め、どの項もの次数は1である。例えばA型では次のようなリー同型が取れる:
\begin{align}e_k =x_k∂_{k+1},f_k=x_{k+1}∂_k\end{align}\begin{align}h_k=x_k∂_k- x_{k+1}∂_{k+1}\end{align}
この埋め込みに関して全く情報がないので、
あれば知りたいのです。
そして本題。行列による表示だと分かりませんが、2階微分作用素への埋め込みも存在する。例えばB型のカルタン行列に対し次の同型が取れる:
\begin{align}e_k=\partial_k x_{k+1},f_k =x_k ∂_{k+1},h_k=-x_k ∂_k +x_{k+1}\partial_{k+1}(1≦k\lt N)\end{align}
\begin{align}e_N=\frac{1}{2}∂_{N}^{2},f_N=\frac{1}{2}x_N^2,h_N=x_N ∂_N+\frac{1}{2}\end{align}
(証明は忙しいので省きます...)
D型も2階の微分を使って表せます。1階の微分だと接空間として考えられますが、2階微分だと一般論はあるんでしょうか??
例外型EFGでも1階の微分では書けますが、2階微分はどうなのか1番知りたいです!